From hexagonal to orthorhombic: AlN > Dr. Probe / Examples

 

We describe the orthogonalization of a hexagonal atomic structure for TEM and STEM image simulations. Orthogonalzation is required for structure models where one of the cell angles is not 90 degrees. The material in this example is aluminum nitride (AlN) and we want to prepare a structure model for imaging along the [001] zone-axis of the crystal by using the program CellMuncher.

Quick guide to structure model orthogonalization

The steps required to orthogonalize a structure model for STEM and TEM image simulations are listed here in short. More detailed explanations are given below.

• Open the Dr. Probe command-line shell and prepare a folder structure for storing data.
• Obtain an initial unit cell or create one with BuildCell.
• Use CellMuncher to create an orthogonal structure model:
  • Swap axis to bring the non-orthogonal plane in the x-z plane.
  • Apply orthogonalization in the x-z plane.
  • Reverse the initial swapping of axes.
  • Wrap atoms into the new periodic unit.
  • Remove close or duplicate atoms from the new cell.

Preparations

• Start the console or command-line shell. On Windows OS you may use the Dr. Probe command-line shell or add the Dr. Probe installation folder to your environmental PATH variable.
• Create a working directory for storing data, e.g. C:\data\aln\001\.
• Switch to this directory within the command-line shell by typing
  cd C:\data\aln\001
  

 

Initial structure file of hexagonal AlN

The example is based on an initial structure data file as given by the text block below. Please copy the text block and save it as file AlN-00.cel or download the initial structure file!

# Super-cell data created by BuildPrimitiveCell   0   0.3110  0.3110  0.4980 90.0000 90.0000 120.0000   N    0.666667  0.333334  0.382100  1.000000  0.003550  0.000000  0.000000  0.000000   N    0.333334  0.666667  0.882100  1.000000  0.003550  0.000000  0.000000  0.000000   Al   0.666667  0.333334  0.000000  1.000000  0.003000  0.000000  0.000000  0.000000   Al   0.333334  0.666667  0.500000  1.000000  0.003000  0.000000  0.000000  0.000000  *

Alternative you may create the structure file with the program BuildCell by the command

BuildCell --spacegroup=186 --lattice=3.110,3.110,4.980,90.0,90.0,120.0 --atom=Al,-0.333333,-0.666667,0.000000,1.0,0.300 --atom=N,-0.333333,-0.666667,0.3821,1.0,0.355 --output=AlN-00.cel

The structure data is taken from H. Schulz & K.H. Thiemann, Solid State Communications 23 (1977) 815-818.

In [001] projection it displays as shown by the image below.

 

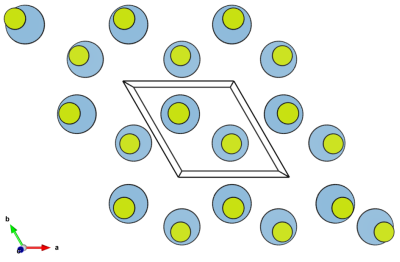
Calculation of the orthogonal cell dimensions

By orthogonalizing a structure model, we try to find a (usually larger) periodic unit of the structure, where all cell axes are oriented with 90 degree angles against each other. In the present example of AlN, where the angle between a- and b-axis is 120 degrees, the orthogonalization is a mere 2-dimensional problem, as illustrated below, because the angles alpha between the x- and z-axis, and beta between the y- and z-axis are both 90 degree already.

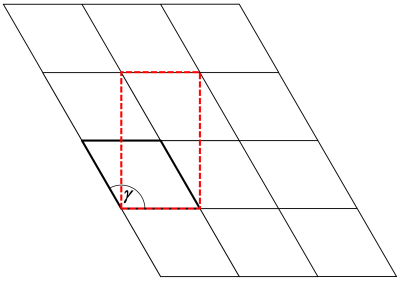
In this case, an orthogonal unit cell is found with the new basis vectors a' = a and b' = 2b - a.

In general, the solution is not alway as simple, in particular, when the angle gamma is not 120 deg, or when the original lattice constants are not equal, i.e. a ≠ b. In such general cases, the solution requires a linear combination with very large multiples of the original lattice vectors to span a perfectly periodic new unit. There are also cases, where even no exact solution exists. It may be possible to finde approximate solutions.

The following sequence of operations with the program CellMuncher will transform the hexagonal AlN structure model into a model with an orthorhombic unit cell.

1. Swap the y- and z-axes of the initial structure, since CellMuncher applies its orthogonalization routine to the plane containing the beta angle only.
   CellMuncher -f AlN-00.cel -o AlN-01.cel --swap-axes=yz

2. Apply the orthogonalization:
   CellMuncher -f AlN-01.cel -o AlN-02.cel --orthogonalize-plane=xz,2
   Note: The number specified at the end of the command-line argument limits the possible periodic repeat of the original cell to find orthogonal substitutions. If no solution is found within this bound, CellMuncher will abort. In this case you should rather use the CellMuncher option --create-block to cut an orthogonal block from the initial structure (see the CellMuncher documentation). The option --create-block is the most direct way of creating an orthogonal super-cell of any given structure. However, it requires a few pre-calculation to select a proper block, depending very much on the details of the input structure.
3. Swap axes again to get back to the original orientation of the structure.
   CellMuncher -f AlN-02.cel -o AlN-03.cel --swap-axes=yz
   In this step, we already obtain the final super-cell of this example, which is now orthogonal and as the size of a = 0.3110 nm, b = 0.5387 nm, and c = 0.4980 nm.
   
4. Since some of the atomic sites may be placed out of the cell bounds, we wrap them back periodically into the range [0,1) for all three dimensions.
   CellMuncher -f AlN-03.cel -o AlN-04.cel --periodic=x --periodic=y --periodic=z
   
5. Finally, we remove close or duplicate atoms from the cell.
   CellMuncher -f AlN-04.cel -o AlN_001.cel --remove-close-atoms=0.2
   The value specified with the option --remove-close-atoms denotes the minimum allowed interatomic distance in the structure. A value of 0.2 Å is usually sufficient.

The structure obtained after the transformtion to an orthorhombic cell is shown below in three different projections.

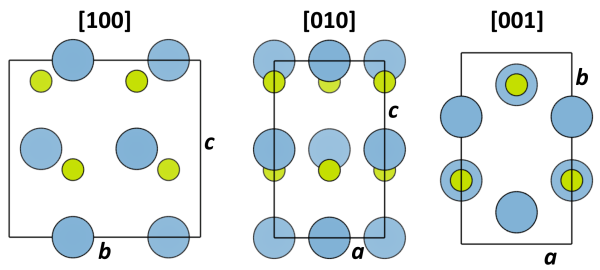
The structure definition file AlN_001.cel obtained after the above transformations to an orthorhombic cell is listed.

# Super-cell data created by BuildPrimitiveCell   0   0.3110  0.5387  0.4980 90.0000 90.0000 90.0000  Al   0.000000  0.666667  0.000000  1.000000  0.003000  0.100000  0.100000  0.100000  N    0.000000  0.666667  0.382100  1.000000  0.003550  0.100000  0.100000  0.100000  Al   0.000000  0.333334  0.500000  1.000000  0.003000  0.100000  0.100000  0.100000  N    0.000000  0.333334  0.882100  1.000000  0.003550  0.100000  0.100000  0.100000  Al   0.500000  0.166667  0.000000  1.000000  0.003000  0.100000  0.100000  0.100000  N    0.500000  0.166667  0.382100  1.000000  0.003550  0.100000  0.100000  0.100000  Al   0.500000  0.833333  0.500000  1.000000  0.003000  0.100000  0.100000  0.100000  N    0.500000  0.833333  0.882100  1.000000  0.003550  0.100000  0.100000  0.100000 *

Summary of commands:

Following is the complete sequence of all commands used above. You may copy this sequence and execute it by one call from a batch file or shell script.

BuildCell --spacegroup=186 --lattice=3.110,3.110,4.980,90.0,90.0,120.0 --atom=Al,-0.333333,-0.666667,0.000000,1.0,0.300 --atom=N,-0.333333,-0.666667,0.3821,1.0,0.355 --output=AlN-00.cel
CellMuncher -f AlN-00.cel -o AlN-01.cel --swap-axes=yz
CellMuncher -f AlN-01.cel -o AlN-02.cel --orthogonalize-plane=xz,2
CellMuncher -f AlN-02.cel -o AlN-03.cel --swap-axes=yz
CellMuncher -f AlN-03.cel -o AlN-04.cel --periodic=x --periodic=y --periodic=z
CellMuncher -f AlN-04.cel -o AlN_001.cel --remove-close-atoms=0.2 --cif


Translation from CEL to CIF for visualization

Use the command

CellMuncher -f dummy-file-name.cel -o dummy-file-name.cif -w CIF

for translating from the CEL file format to CIF. You can open the resulting CIF file directly with the program VESTA to visualize the structure.

Note that the B_iso values in the CIF output of CellMuncher is on a wrong scale. Correct these values before using the CIF file in simulations.

 

Last update: Jan 26, 2019    contact    disclaimer(de)